Answer:
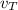 = 4.35 m/s
= 4.35 m/s
Explanation: Drag Force opposes the motion of an object and depends on shape, size, velocity of the object or person and the fluid it is in.
Terminal velocity occurs when gravitational force and drag force are equal, which gives a net force and acceleration of zero. At that moment, velocity is constant and called terminal.
Terminal velocity is found by the following formula:
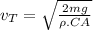
ρ is density of the fluid
C is drag coefficient
A is area of the object in which forces are acting
The paratrooper and his parachute weighs 1000N, so this means
mg = 1000
Drag coefficient of a parachute is an average of C = 1.75
A parachute is half an sphere. So, area is
![A=0.5[4.\pi.r^(2)]](https://img.qammunity.org/2021/formulas/physics/college/fhqo83gpvkce90jixkrtd7fd4j8u9twa8k.png)
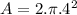
A = 16π m²
Substituing:
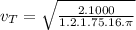
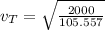
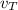 = 4.35
= 4.35
The terminal velocity of the paratrooper is 4.35m/s