Question

the period of the satellite is exact 42.391 hours, the earth's mass is 5.98 kg and the radius of th earth is 3958.8 miles, what is the distance of the satellite from the surface of the earth in miles?

Answer 1

As the mass is not written well, i will use the equation in terms of the gravitational acceleration:

The equation for the period of a satellite is:

`T = 2*pi*\sqrt{(r^3)/(g*R^2) }`

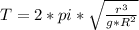
We want to find r, so isolating r we get:

`r = \sqrt[3]{x ((T)/(2*pi) )^2*g*R^2}`

Where:

T = period.

r = radius of the satellite.

R = radius of the planet.

g = gravitational acceleration of the planet.

pi = 3.14159...

g = 78999.64 mi/h^2 (value of a table)

T = 42.391 h.

R = 3958.8 miles

We can replace those values in the equation and get:

`r = \sqrt[3]{ ((42.391)/(2*3.14159) )^2*78999.64*(3958.8)^2} = 38,339.5 mi`

Now this value is measured from the center of the Earth, then the altitude of the satellite measured from the surface of the Earth will be:

H = r - R = 38,339.1mi - 3958.8mi = 34,380.3 mi