Answer: 0.3964
Explanation:
Given: A particular fruit's weights are normally distributed, with a mean
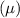 of 230 grams and a standard deviation
of 230 grams and a standard deviation
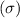 of 37 grams.
of 37 grams.
Sample size : n= 87
Let
 be the sample mean.
be the sample mean.
The probability that their mean weight will be between 231 grams and 240 grams will be :
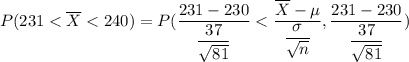
![=P(0.2432<Z<2.4324)\ \ \ \ [Z=\frac{\overline{X}-\mu}{(\sigma)/(√(n))}]\\\\=P(Z<2.4324)-P(Z<0.2432)\\\\=0.9925- 0.5961=0.3964](https://img.qammunity.org/2021/formulas/mathematics/college/hhmwf2j8108qw1ryccwrf8i5yxvmbr4tgv.png)
Hence, the required probability = 0.3964