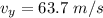Question

9, You are piloting a helicopter which is man vertically at a un

you reach 196.00 m,

velocity of 8.50 m/

a) When does th

14.70 m/s. When

a horizontal

B vertically ata uniform velocity of 14.70 m/s

ach 196.00 m, you see Barney (Uh-oh). A la

1. A large object is projected with a horizon

city of 8.50 m/s from the rising helicopter.

Vhen does the ball reach Barney's head if he

ad if he is standing in a hole with his head at

level? (7.99 s]

b) Where do

have to be horizontally relative to the helicopter's position? (68.0 ml

city when it hits the ground? - 63.7 m/s]

c) What is the vertical velocity when it hits the

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

a

t = 8 seconds

b

`D = 68 \ m`

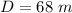
c

`v_y = 63.7 \ m/s`

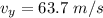
Step-by-step explanation:

From the question we are told that

The initial uniform velocity is
`v =14.70 \ m/s`

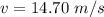
The height considered is
`s = 196.00 \ m`

The speed of the large object is
`v = 8.50 \ m/s`

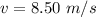
Generally according to the equation of motion

`s = -ut + (1)/(2) gt^2`

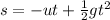
Here u is negative because the helicopter is moving upward against gravity

`196= -14.7 t + (1)/(2) 9.8 t^2`

=>
`4.9 t^2 - 14.7t -196 = 0`

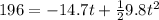
solving this using quadratic equation formula we obtain that

t = 8 seconds

So the time taken for the large object to hit Barney is t = 8 seconds

Gnerally the horizontal distance of Barney relative to the helicopter is mathematically represented as

`D = v * t`

`D = 8.5 * 8`

`D = 68 \ m`

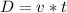
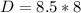
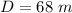
generally given that Barney head is the same level with the ground then the vertical velocity when it hits the ground is mathematically represented as

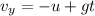
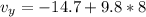
`v_y = -u +gt`

=>
`v_y = -14.7 +9.8 * 8`

=>
`v_y = 63.7 \ m/s`