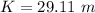Answer:
The drawdown at the midpoint is
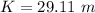
Step-by-step explanation:
From the question we are told that
The transmissivity is

The diameter is

The storativity is
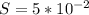
The distance of the vault from the pumping well is
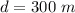
The pumping rate is
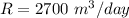
Generally the radius is mathematically represented as
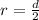
=>
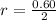
=>

Generally the time is 1 year = 365 days as stated in the question
Generally the drawdown at the midpoint between the fault and the well is mathematically represented as
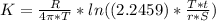
=>

=>