Question

g if 2 half-lives elapsed in a rock containing Carbon-14 and Nitrogen-14, what is the ratio of parent to daughter isotopes

Answer 1

The ratio of parent to daughter isotopes is
`(1)/(3)`.

Step-by-step explanation:

We know that Carbon-14 decays in time and transforms into Nitrogen-14, being the latter the "daughter" of the first one. The decay of any isotope is represented by the following ordinary linear differential equation:

`(dm)/(dt) = -(m)/(\tau)` (Eq. 1)

Where:

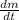`(dm)/(dt)` - Rate of change of the isotope mass, measured in grams per year.

`\tau` - Time constant, measured in years.

`m` - Current mass of the isotope, measured in grams.

The solution of this differential equation is:

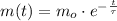`m(t) = m_(o)\cdot e^{-(t)/(\tau) }` (Eq. 2)

Where:

`t` - Time, measured in years.

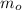`m_(o)` - Initial mass of the isotope, measured in grams.

Time constant can be found as a function of half life. Please notice that half-life of Carbon-14 is 5760 years. The equation of time constant is:

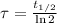`\tau = (t_(1/2))/(\ln 2)` (Eq. 3)

Where
`t_(1/2)` is the half-life of the isotope, measured in years.

If we know that
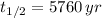`t_(1/2) = 5760\,yr` and
`t = 2\cdot t_(1/2)`, then we have that:

`\tau = (5760\,yr)/(\ln 2)`

`\tau \approx 8309.923\,yr`

`m(t) = m_(o)\cdot e^{-(2\cdot (5760\,yr))/(8309.923\,yr) }`

`m = 0.25\cdot m_(o)`

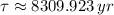
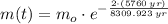
Which means that 75 % of the original mass of Carbon-14 became Nitrogen-14. The parent-to-daughter ratio is:

`r = (0.25\cdot m_(o))/(0.75\cdot m_(o))`

`r = (1)/(3)`

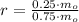
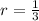
The ratio of parent to daughter isotopes is
`(1)/(3)`.