Question

Past records indicate that 10% of online retail orders are fraudulent. Suppose 20 online orders are placed. What is the probability that none are fraudulent

Answer 1

`Probability = 0.1216`

Explanation:

Given

`n = 20`

Represent fraudulent with p

`p = 10\%`

`p = 0.10`

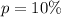
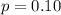
Required

Determine the probability that none are fraudulent

First, we need to determine the proportion of those that are not fraudulent.

Represent this with q

`p + q= 1`

`10\% + q = 1`

`q = 1 - 10\%`

`q = 90\%`

`q = 0.9`

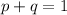
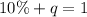
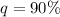
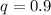
The required probability is binomial and can be determine using the following:

`(p + q)^n = ^nC_xp^xq^(n - x); x = 0,1,2...n`

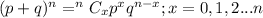
In this case x = 0 (none);

So, the required probability is:

`Probability = ^nC_0p^0q^(n - 0)`

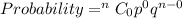
Substitute values for n, p and q

`Probability = ^(20)C_0 * 0.1^0 * 0.9^(20 - 0)`

`Probability = ^(20)C_0 * 0.1^0 * 0.9^(20)`

`Probability = ^(20)C_0 * 1* 0.9^(20)`

`Probability = (20!)/((20 - 0)!20!) * 1* 0.9^(20)`

`Probability = 1 * 1* 0.9^(20)`

`Probability = 0.9^(20)`

`Probability = 0.12157665459`

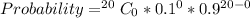
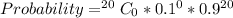
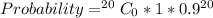
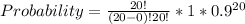
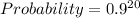
`Probability = 0.1216` Approximated