Question

Consider an ionic compound, MXMX , composed of generic metal MM and generic, gaseous halogen XX . The enthalpy of formation of MXMX is ΔH∘f=−421ΔHf∘=−421 kJ/mol. The enthalpy of sublimation of MM is ΔHsub=155ΔHsub=155 kJ/mol. The ionization energy of MM is IE=401IE=401 kJ/mol. The electron affinity of XX is ΔHEA=−321ΔHEA=−321 kJ/mol. (Refer to the hint). The bond energy of X2X2 is BE=239BE=239 kJ/mol. Determine the lattice energy of MXMX .

Answer 1

- 775.5 kJ/mol

Step-by-step explanation:

Given that:

The enthalpy of formation of MX is
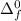`\Delta_f^0` = - 421 kJ/mol

The enthalpy of sublimation of MM is
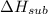`\Delta H_(sub)` = 155 kJ/mol

The ionization energy of MM is = 401 kJ/mol

The electron affinity of XX is
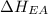`\Delta H_(EA)` = -321 kJ/mol

The bond energy of X2 is BE = 239 J/mol

The process for each above component is shown below:

`M_(s) \to M_((g)) ---> ( \Delta H_(sub) = 155 \ kJ/mol})`

`(1)/(2)X_(2(g)) \to X_((g)) ---> ( BE = (239)/(2) kJ/mol ) = (119.5 kJ/mol )`

`M_((g)) \to M^+_((g)) + e^- ---> ( IE_1 = 401 \ kJ/mol )`

`X_((g)) + e^- --> X^-_((g)) ---> ( \Delta H_(EA )= -321 \ kJ/mol )`

`M^+_((g)) +(1)/(2)X^-_((g)) \to MX ---> ( \Delta H^0_f = -421 \ kJ/mol )`

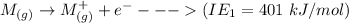
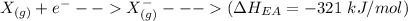
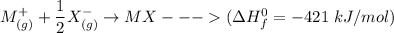
Thus, the overall reaction is:

`M_((s))+ (1)/(2)X_(2(g)) \to MX_((s))`

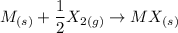
The overall energy is:

`\mathtt{\Delta H^0_f = U + \Delta H_(sub) + IE + BE + \Delta H_(EA )}`

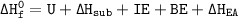
- 421 kJ/mol = U + 155 kJ/mol + 401 kJ/mol + 119.5 kJ/mol + (-321 kJ/mol)

- 421 kJ/mol = U + 354.5 kJ/mol

- U = 421 kJ/mol + 354.5 kJ/mol

- U = 421 kJ/mol + 354.5 kJ/mol

- U = 775.5 kJ/mol

U = - 775.5 kJ/mol

Thus, the lattice energy of MX (U) = - 775.5 kJ/mol