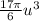Answer:
The volume is 17π/6
Explanation:
We are going to apply first the shell method where the slice is parallel to the axis of revolution, then we need to determine the medium radius ahd the height of the shell, in this case as the region is rotated about the y-axis
 and the height is
and the height is
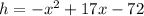
Then the integral is
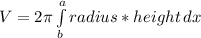
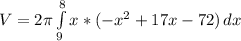
![V=2\pi [-(x^(4) )/(4) +(17)/(3)x^(3)-36x^(2) ]_8^9](https://img.qammunity.org/2021/formulas/mathematics/college/d58zjmomirfy5vaisr570b8pfvaiflptk1.png)
![V=2\pi [-(2465)/(4)+(3689)/(3)-612 ]](https://img.qammunity.org/2021/formulas/mathematics/college/xma8f6qocq3o66tmn67i1go46kru916y78.png)
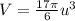
To show the answer we can apply the ring method where the the inner radius is
 and the outter radius
and the outter radius
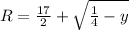
The formula is
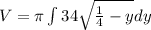 evaluated between
evaluated between
 and
and
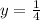
Solving the integral we can get the same solution of
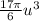
Finally, the volumen is