Question

assume the earths mass is 34.102 kg, and the radius is 56.867 x 10^3 miles, what would be the gravitational acceleration on such an planet in unit of m/s^2?

Answer 1

The gravitational acceleration of that planet is
`2.718* 10^(-25)` meters per square second.

Step-by-step explanation:

Under the assumption that Earth is a sphere and with an uniformly distributed density, the gravitational acceleration at the surface of the planet is given by the following expression:

`g = G\cdot (M)/(r^(2))` (Eq. 1)

Where:

`G` - Gravitation constant, measured in newton-square meters per square kilogram.

`r` - Radius of the planet, measured in meters.

`M` - Mass of the planet, measured in kilograms.

If we know that
`M = 34.102\,kg`,
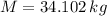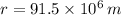`r = 91.5* 10^(6)\,m` and
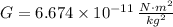`G = 6.674* 10^(-11)\,(N\cdot m^(2))/(kg^(2))`, then the acceleration on the planet is:

`g = \left(6.672* 10^(-11)\,(N\cdot m^(2))/(kg^(2)) \right)\cdot \left[(34.102\,kg)/((91.5* 10^(6)\,m)^(2)) \right]`

`g = 2.718* 10^(-25)\,(m)/(s^(2))`

The gravitational acceleration of that planet is
`2.718* 10^(-25)` meters per square second.