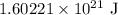Answer:
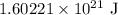
Step-by-step explanation:
 = Density of sattelite =
= Density of sattelite =
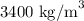
 = Velocity of asteroid =
= Velocity of asteroid =

Radius of the asteroid =
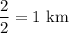
Mass of asteroid
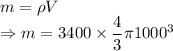
Energy of the asteroid would be
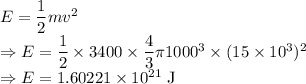
The destructive energy that could be released when the asteroid embeds itself in the Earth is