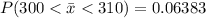Question

What is the probability that the mean overall physical activity level of the sample is between 300 and 310​ cpm? ​P(300​310) nothing ​

Answer 1

Complete Question

In a study on the physical activity of young? adults, pediatric researchers measured overall physical activity as the total number of registered movements? (counts) over a period of time and then computed the number of counts per minute? (cpm) for each subject. The study revealed that the overall physical activity of obese young adults has a mean of mu = 322 cpm and a standard deviation of 80 cpm

In a random sample of n=100 what is the probability that the mean overall physical activity level of the sample is between 300 and 310​ cpm? ​P(300​310) nothing ​

Answer:

The probability is
`P(300 < \= x < 310) = 0.06383`

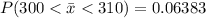
Explanation:

From the question we are told that

The mean is
`\mu = 322 \ cpm`

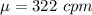
The standard deviation is
`\sigma = 80 \ cpm`

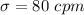
The sample size is
`n = 100`

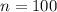
Generally the standard error of the mean is mathematically represented as

`\sigma_(\= x) = (\sigma)/(√(n) )`

=>
`\sigma_(\= x) = (80)/(√(100) )`

=>
`\sigma_(\= x) = 8`

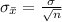
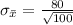
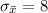
Generally the probability that the mean overall physical activity level of the sample is between 300 and 310​ cpm is mathematically represented as

`P(300 < \= x < 310) = P((300 - 322)/(8) < ( \= x - \mu )/(\sigma_(\= x)) < (310 - 322)/(8) )`

=>
`P(300 < \= x < 310) = P(-2.75 < ( \= x - \mu )/(\sigma_(\= x)) < -1.5 )`

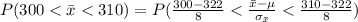
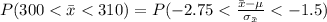
Generally
`(\= x -\mu)/(\sigma )  =  Z (The  \ standardized \  value\  of  \ \= x )`

=>
`P(300 < \= x < 310) = P(-2.75 < Z< -1.5 )`

=>
`P(300 < \= x < 310) = P(Z < -1.5) - P( Z< -2.75 )`

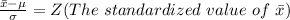
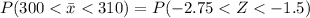
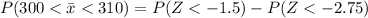
Generally the probability of (Z < -2.75) and ( Z< -1.5 )

`P(Z < -2.75) = 0.0029798`

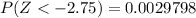
and

`P(Z < -1.5 ) = 0.066807`

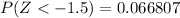
So

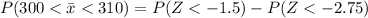
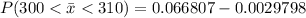
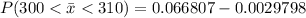
`P(300 < \= x < 310) = P(Z < -1.5) - P( Z< -2.75 )`

=>
`P(300 < \= x < 310) = 0.066807 - 0.0029798`

=>
`P(300 < \= x < 310) = 0.066807 - 0.0029798`

=>
`P(300 < \= x < 310) = 0.06383`