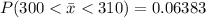Complete Question
In a study on the physical activity of young? adults, pediatric researchers measured overall physical activity as the total number of registered movements? (counts) over a period of time and then computed the number of counts per minute? (cpm) for each subject. The study revealed that the overall physical activity of obese young adults has a mean of mu = 322 cpm and a standard deviation of 80 cpm
In a random sample of n=100 what is the probability that the mean overall physical activity level of the sample is between 300 and 310 cpm? P(300310) nothing
Answer:
The probability is
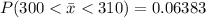
Explanation:
From the question we are told that
The mean is
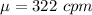
The standard deviation is
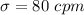
The sample size is
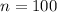
Generally the standard error of the mean is mathematically represented as
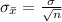
=>
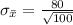
=>
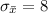
Generally the probability that the mean overall physical activity level of the sample is between 300 and 310 cpm is mathematically represented as
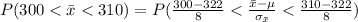
=>
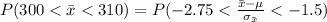
Generally
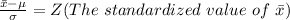
=>
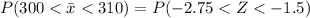
=>
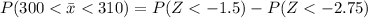
Generally the probability of (Z < -2.75) and ( Z< -1.5 )
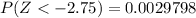
and

So
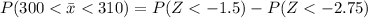
=>

=>

=>