Question

At what height in kilometers above the surface of the Earth is there a 7% difference between the approximate gravitational force mg and the actual gravitational force on an object

Answer 1

There is a 7 % difference between the approximate gravitational force and the actual gravitational force at a height of 240 kilometers.

Step-by-step explanation:

We can calculate gravity as a function of mass of the Earth (
`M`), measured in kilograms, radial distance from center of the planet (
`r`), measured in meters, and gravitation constant (
`G`), measured in newton-square meters per square kilogram:

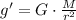`g' = G\cdot (M)/(r^(2))` (Eq. 1)

And we solve the equation for
`r`:

`r =\sqrt{(G\cdot M)/(g') }` (Eq. 1b)

If we know that
`G = 6.674* 10^(-11)\,(N\cdot m^(2))/(kg^(2))`,
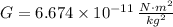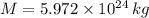`M = 5.972* 10^(24)\,kg` and
`g' = 9.121\,(m)/(s^(2))`, the radial distance from the center of the Earth is:

`r = \sqrt{((6.674* 10^(-11)\,(N\cdot m^(2))/(kg^(2)) )\cdot (5.972* 10^(24)\,kg))/(9.121\,(m)/(s^(2)) ) }`

`r \approx 6.611* 10^(6)\,m`

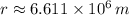
The height above the surface of the Earth is the difference between the value above and the radius of the planet. That is:

`h = 6.611* 10^(6)\,m - 6.371* 10^(6)\,m`

`h = 2.40* 10^(5)\,m` (
`240\,km`)

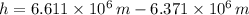
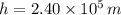There is a 7 % difference between the approximate gravitational force and the actual gravitational force at a height of 240 kilometers.