Question

He function f f is given by f(x)=0.1x4−0.5x3−3.3x2+7.7x−1.99 f ( x ) = 0.1 x 4 − 0.5 x 3 − 3.3 x 2 + 7.7 x − 1.99 . For how many positive values of b b does limx→bf(x)=2 lim x → b f ( x ) = 2 ?

Answer 1

3

Explanation:

We are given that

`f(x)=0.1x^4-0.5x^3-3.3x^2+7.7x-1.99`

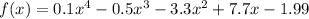
We have to find the positive value of b.

`\lim_(x\rightarrow b)f(x)=2`

`\lim_(x\rightarrow b)(0.1x^4-0.5x^3-3.3x^2+7.7x-1.99)=2`

`0.1b^4-0.5b^3-3.3b^2+7.7b-1.99=2`

`0.1b^4-0.5b^3-3.3b^2+7.7b-1.99-2=0`

`0.1b^4-0.5b^3-3.3b^2+7.7b-3.99=0`

`10b^4-50b^3-330b^2+770b-399=0`

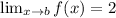
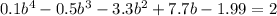
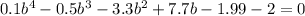
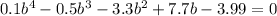
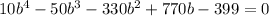
Let

`g(b)=10b^4-50b^3-330b^2+770b-399`

Using Discartes' rule of sign

There are number of sign changes are 3.

Therefore, the positive real roots are 3 or 1.

`g(-b)=10b^4+50b^3-330b^2-770b-399`

There are number of sign changes are 1 .

Therefore, negative real roots are 1.

When negative root is 1 .Then , positive real roots are 3 because total number of roots are 4.

Hence, positive values of b=3