Answer:

Explanation:
Given the expression:

We are to express it as difference of two square (u+v)(u-v). According to the rule:
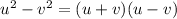
We need to express
 as difference of squares and this is as shown:
as difference of squares and this is as shown:
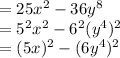
From the resulting expression we can say:
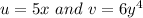
If we substitute in the rule above we will have:
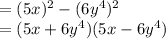
Hence the expression expressed as difference of two square is:
