Question

Each tile has length 1/3 in. And width 1/4 in. The actual tiles have length 1/4 ft and width of 3/16 ft. What is the ratio of the length of a tile in the model to the lenfth of an actual tile? What is the ratio of the area of a tile the model to the area of an actual tile? Describe two ways to find each ratio

Answer 1

Given:

Model tile length =
`(1)/(3)\text{ in.}`

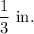
Model tile width =
`(1)/(4)\text{ in.}`

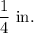
Actual tile length =
`(1)/(4)\text{ ft.}`

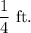
Actual tile width =
`(3)/(16)\text{ ft.}`

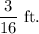
To find:

The ratio of the length of a tile in the model to the length of an actual tile and the ratio of the area of a tile the model to the area of an actual tile.

Solution:

We know that,

1 ft = 12 in.

Actual tile length
`=(1)/(4)* 12\text{ in.}`

`=3\text{ in.}`

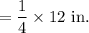
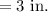
Actual tile width
`=(3)/(16)* 12\text{ in.}`

`=(3)/(4)* 3\text{ in.}`

`=(9)/(4)\text{ in.}`

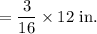
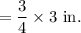
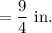
The ratio of the length of a tile in the model to the length of an actual tile is

`((1)/(3))/(3)=(1)/(9)=1:9`

Therefore, the ratio of the length of a tile in the model to the length of an actual tile is
`(1)/(9)` or it can be written as 1:9.

Area of rectangle = length × width

Area of model tile
`=(1)/(3)* (1)/(4)`

`=(1)/(12)\text{ in.}^2`

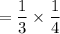
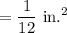
Area of actual tile
`=3* (9)/(4)`

`=(27)/(4)\text{ in.}^2`

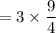
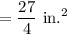
The ratio of the area of a tile the model to the area of an actual tile is

`((1)/(12))/((27)/(4))=(1)/(12)* (4)/(27)`

`((1)/(12))/((27)/(4))=(1)/(3)* (1)/(27)`

`((1)/(12))/((27)/(4))=(1)/(81)=1:81`

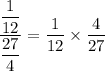
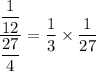
Therefore, ratio of the area of a tile the model to the area of an actual tile is
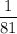`(1)/(81)` or it can be written as 1:81.