Answer:
So the change will be express as a difference of both electric potential:
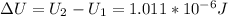
Step-by-step explanation:
The electric potential is given by:
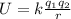
The electric potential at a distance of 2.3 cm will be:
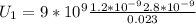
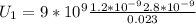

Now, the electric potential when the first particle has moved 1.0 cm is.
Here, the distance between the two particles will be 2.3 cm - 1 cm = 1.3 cm
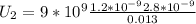
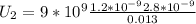
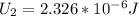
So the change will be express as a difference of both electric potential:
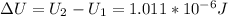
I hope it helps you!