Question

At a certain fire station, false alarms are received at a mean rate of 0.2 per day. In a year, what is the probability that fewer than 60 false alarms are received? (Consider 365 days a year. Round your standard deviation value to 3 decimal places and z-value to 2 decimal places. Round your final answer to 4 decimal places.)

Answer 1

The probability that fewer than 60 false alarms are received is 0.0643.

Explanation:

Let X denote the number of false alarms received at a certain fire station in a year.

The mean rate of false alarms in a day is 0.20.

Then the mean rate of false alarms in a year will be:
`365* 0.20=73`.

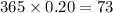Then the random variable X follows a Poisson distribution with parameter λ = 73.

The Poisson distribution with parameter λ, can be approximated by the Normal distribution, when λ is large.

If X follows Poisson (λ) and λ is large then the distribution of X can be approximated but he Normal distribution.

The mean of the approximated distribution of X is:

μ = λ

The standard deviation of the approximated distribution of X is:

σ = √λ

Thus, if λ is large, then X follows N (μ = λ, σ² = λ).

Compute the mean and standard deviation of X as follows:

`\mu=\lambda=73\\\\\sigma=√(\lambda)=√(73)=8.544`

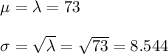
Compute the probability that fewer than 60 false alarms are received as follows:

`P(X<60)=P((X-\mu)/(\sigma)<(60-73)/(8.544))`

`=P(Z<-1.52)\\\\=0.06426\\\\\approx 0.0643`

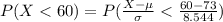
Thus, the probability that fewer than 60 false alarms are received is 0.0643.