Question

An adiabatic piston-cylinder compressor has an efficiency of 85%. If air is compressed from 101 kPa and 25 o C to 1200 kPa. Determine the actual work done and the actual final temperature. g

Answer 1

`T_2=604.70K=331.55\°C`

`W=220.10(J)/(g)`

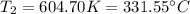
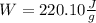
Step-by-step explanation:

Hello!

In this case, for this compression of air from 101 kPa to 1200 kPa, we should first realize that equation relating P and T is:

`T_1*P_1^{(1-\gamma)/(\gamma) }=T_2*P_2^{(1-\gamma)/(\gamma) }`

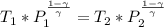
Whereas:

`\gamma=(Cp_(air))/(Cv_(air)) =(1.00J/(g\°C))/(0.718J/(g\°C))=1.40`

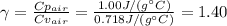
That is why the final temperature is:

`T_2=T_1((P_1)/(P_2))^{(1-\gamma)/(\gamma) }\\\\T_2=298.15K((101kPa)/(1200kPa))^{(1-1.40)/(1.40) }\\\\T_2=604.70K=331.55\°C`

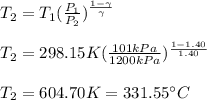
Moreover, for the work done, since the process is adiabatic, no heat is in the equation:

`Q-W=\Delta U`

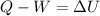
But as the work is done on the system we can write:

`-(-W)=\Delta U=Cv(T_2-T_1)\\\\W=0.718(J)/(g*K)(604.70K-298.15K)\\ \\W=220.10(J)/(g)`

Best regards!