Question

A crystal mth a simple cubic lattice and a monoatomic basis has an atomic ra- dius of 2.5 A and an atomic weight of 5.42. Calculate its density, assuming that the atoms touch each other.

Answer 1

density = 0.071984 g/cm³

Step-by-step explanation:

For a simple cubic lattice structure;

There are 8 atoms in the unit cell, with each edge of the cell contributing 1/8th atom to one unit cell.

Thus, in a unit cell, the required number of atoms = 8/8 = 1

The mass of the unit cell can be calculated by using the formula:

`Mass \ of \ the \ unit \ cell = (no \ of atoms \ * Atomic \ weight )/(Avogadro \ No)`

`Mass \ of \ the \ unit \ cell = (1 \ * 5.42 )/(6.023* 10^(23))`

`Mass \ of \ the \ unit \ cell = 8.998 * 10^(24 ) \ g`

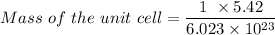
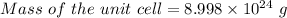
Similarly, given the atomic radius = 2.5 angstrom =
`2.5 * 10^(-10) \ meter`

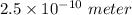
Thus, volume V = a³

The edge length for the simple cubic radius is:

a = 2 × r

a = 2 ×
`2.5 * 10^(-10)`

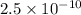
a =
`5 * 10^(-10)` m

a =
`5 * 10^(-8) \ cm`

Now;

volume V = a³

volume V =
`(5 * 10^8)^3`

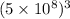
volume V =
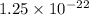`1.25 * 10^(-22)` cm³

Finally; the density = mass/volume

density =
`(8.998 * 10^(-24))/(1.25 * 10^(-22))`

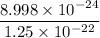
density = 0.071984 g/cm³