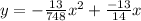Question

Jeremy stands on the edge of a river and throws a rock into the water. The rock leaves his hand at a height 4 feet above the water. The rock reaches the highest point along its path when it is a horizontal distance of 28 feet from his hand and 17 feet above the water. Write a function to represent the height of the rock in terms of its distance from Jeremy's hand.

Answer 1

`y=-\frac {13}{748}x^2+(13)/(14)x`

Explanation:

Let the initial position of rock (in hand) is the origin.

Given that the rock reaches the highest point along its path when it is a horizontal distance of 28 feet from his hand and 17 feet above the water.

Let x and y be the horizontal distance from hand and the height from hand.

As the trajectory of the path of the rock in the gravitational field is parabolic and parabolic equations is represented by the quadratic equation.

So, let the equation of path of the rock is

`y=ax^2+bx+c\cdots(i)`

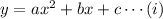
Where a, b, and c are constants.

At the initial point, y=0 and x=0

So, from equation (i),

`c=0\cdots(ii)`

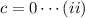
As the position of the hand is 4 feet above the water, so, at x= 28 feet,

y = 17-4 = 13 feet.

From equation (i) and (ii),

`13=28^2a+28b\cdots (iii)`

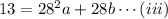
Now, at the highest point, x=28 feet, the rate of change of the hight is zero, i.e the slope of the curve is zero, so

at
`x=28, (dy)/(dx)=0`

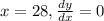
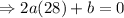`\Rightarrow 2a(28)+b=0` [from (i)]

`\Rightarrow b=-56a\cdots(iv)`

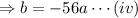
From equations (iii) and (iv),

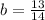`b=(13)/(14)` and

`a=\frac {-13}{784}`

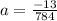
Put the values of a, b, and c in the equation (i), we have

`y=-\frac {13}{748}x^2+(-13)/(14)x`

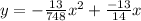
Hence, the function to represent the height of the rock, y, in terms of its distance from Jeremy's hand, x. is

`y=-\frac {13}{748}x^2+(-13)/(14)x`