Question

Thompson and Thompson is a steel bolts manufacturing company. Their current steel bolts have a mean diameter of 145145 millimeters, and a standard deviation of 77 millimeters. If a random sample of 3131 steel bolts is selected, what is the probability that the sample mean would differ from the population mean by greater than 33 millimeters

Answer 1

The probability that the sample mean would differ from the population mean by greater than 33 millimeters is 0.0174

Explanation:

`Mean = \mu = 145 mm`

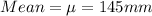
Standard deviation =
`\sigma = 7`

We are supposed to find the probability that the sample mean would differ from the population mean by greater than 3 millimeters

`P(|x-\mu|>33)=1-P(|x-\mu|<3)\\P(|x-\mu|>33)=1-P(-3<|x-\mu|<3)\\P(|x-\mu|>33)=1-P((-3)/((\sigma)/(√(n)))<(|x-\mu|)/((\sigma)/(√(n)))<(-3)/((\sigma)/(√(n))))\\P(|x-\mu|>33)=1-P((-3)/((7)/(√(31)))<(|x-\mu|)/((\sigma)/(√(n)))<(-3)/((7)/(√(31))))\\P(|x-\mu|>33) =1-P(-2.38<z<2.38)\\P(|x-\mu|>33) =1-(P(z<2.38)-P(z<-2.38))\\`

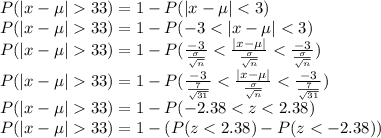
Using Z table

= 1-(0.9913-0.0087)

=0.0174

Hence the probability that the sample mean would differ from the population mean by greater than 33 millimeters is 0.0174