Answer:
The dimensions of the aquarium that minimize the cost of the materials:
![x=y=\sqrt[3]{(2V)/(5)}\\z=\sqrt[3]{(25V)/(4)}](https://img.qammunity.org/2021/formulas/mathematics/college/f09gygzj15fyzr2r2tgtxj5c95imm1yzug.png)
Explanation:
Let x, y and z be the dimensions of aquarium .
Surface area of an aquarium = xy+2yz+2xz
Volume of aquarium V=
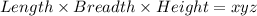 ----A
----A
We are given that slate costs five times as much (per unit area) as glass
So, Cost function : C=5xy+2yz+2xz
Now we will use langrage multiplier to find the dimensions of the aquarium that minimize the cost of the materials.
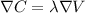
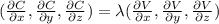

So,
 ----1
----1
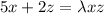 -----2
-----2
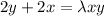 ----3
----3
Multiply 1 ,2 and 3 by x,y and z respectively.
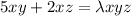 ----4
----4
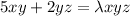 -----5
-----5
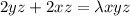 ----6
----6
Now equate 4 and 5
5xy+2xz=5xy+2yz
x=y
Substitute y=x in 5 and 6 and equate them
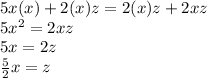
Substitute the values in A
![V = xyz = x * x * (5)/(2)xV=(5)/(2)x^3\\\sqrt[3]{(2)/(5)V}=x\\x=y=\sqrt[3]{(2)/(5)V}\\z=(5)/(2)x=(5)/(2)(\sqrt[3]{(2)/(5)})=\sqrt[3]{(25V)/(4)}](https://img.qammunity.org/2021/formulas/mathematics/college/lozr718x87o329xhaq42gov2i4nysh5fqc.png)
Hence,
The dimensions of the aquarium that minimize the cost of the materials:
![x=y=\sqrt[3]{(2V)/(5)}\\z=\sqrt[3]{(25V)/(4)}](https://img.qammunity.org/2021/formulas/mathematics/college/f09gygzj15fyzr2r2tgtxj5c95imm1yzug.png)