Answer:

Explanation:
We are given that
Height of tank=6feet
Diameter of tank=8 feet
Radius of cone,r=d/2=8/2=4 feet
Let a layer of thickness dy at distance yr from the bottom at origin
y=6 feet
Using similar triangle property
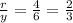
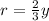
Weight of water=62.4 pounds per cubic foot
Now,
Weight of layer=
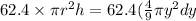
Now, work done to fill the tank from a depth of 4 feet to a depth of 6 feet is given by

![W=(62.4* 4\pi)/(9)[(y^4)/(4)]^(6)_(4)](https://img.qammunity.org/2021/formulas/mathematics/college/vnskom46agutvoo2bhyvojudqgogagglgw.png)

