Question

Molecules of a toxic chemical eventually decompose into inert substances. Suppose the decomposition time is exponentially distributed with a mean of 1/lambda. The half-life of such a persistent poison is that time beyond which the probability is .50 that a particular molecule will remain toxic. Find the half-life for chemicals whose molecules have an average decomposition time of

Answer 1

a)4.15 years

b)22.18 years

c)188.53 years

d)3027.66 years

Explanation:

Formula :
`P(X\leq t)=1-e^{(-t)/(\lambda)}`

So,
`P(X>t)=1-(1-e^{(-t)/(\lambda)})`

`P(X>t)=e^{(-t)/(\lambda)}`

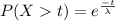
We are given that The half-life of such a persistent poison is that time beyond which the probability is .50 that a particular molecule will remain toxic i.e. P(X>t)=0.5

So,
`e^{(-t)/(\lambda)}=0.5`

Taking natural log both sides

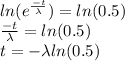
`ln(e^{(-t)/(\lambda)})=ln(0.5)\\(-t)/(\lambda)=ln(0.5)\\t=-\lambda ln(0.5)`

a)

`\lambda =6`

t=-(6) ln(0.5)=4.15 years

b)

`\lambda =32`

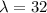
t=-(32) ln(0.5)=22.18 years

c)

`\lambda =272`

t=-(272) ln(0.5)=188.53 years

d)

`\lambda =4368`

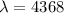
t=-(4368) ln(0.5)=3027.66 years