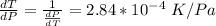Answer:
The answer is
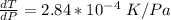
Step-by-step explanation:
From the question we are told that
The boiling point of water is

The enthalpy of vaporization is
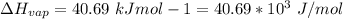
The molar volume of liquid water is

The molar volume of steam is
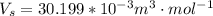
The pressure is
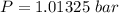
Gnerally from Clausius Clapeyron equation we have that
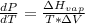
Here
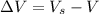
=>
![\Delta V = [30.199 * 10^(-3) ] - [ 0.019 * 10^(-3)]](https://img.qammunity.org/2021/formulas/chemistry/college/7jivyfyr0kxz9kbn185wlzfl2q2v1g3ea3.png)
=>
![\Delta V = [30.199 * 10^(-3) ] - [ 0.019 * 10^(-3)]](https://img.qammunity.org/2021/formulas/chemistry/college/7jivyfyr0kxz9kbn185wlzfl2q2v1g3ea3.png)
=>
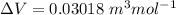
So
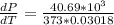
=>
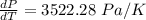
Generally from the we are ask to obtain the change in the boiling point of water at 1000 C per Pa change under atmospheric pressure conditions which is mathematically represented as
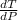
So

=>