Question

Terrence drove to his sister's house, a distance of d miles. For the first 150 miles, he was able to drive relatively quickly, at 60 miles per hour. For the remaining distance, the road was rougher, and he had to slow his speed by 20 miles per hour. For each part of the journey, he was able to keep a steady speed. The time he spent driving at the faster speed was twice the time he spent driving at the slower speed.

Answer 1

The total distance he drove is 350 miles, with an average speed of 46.67 miles/hour.

Explanation:

Let
`t_1` and
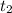`t_2` be the time of driving at a slower rate and at a faster rate respectively.

Given that the total distance = d

The speed for the first 150 miles = 60 miles/hour.

So,
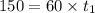`150=60* t_1` [ as distance = speed x time]

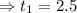`\Rightarrow t_1=2.5` hours.

The remaining distance
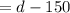`= d-150` miles.

Speed for the remaining distance = 60 miles/hour.

As the time he spent driving at the faster speed was twice the time he spent driving at the slower speed,

So, the time of driving at a faster rate,
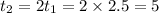`t_2 = 2t_1=2*2.5=5` hours

So,
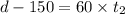`d-150=60* t_2` [ as distance = speed x time]

`\Rightarrow d-150=20* 5=100`

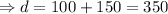`\Rightarrow d = 100+150=350` miles.

The average speed of the journey = (Total distance)/(Total time taken )

`=d/(t_1+t_2)`

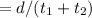
=350/(2.5+5)

=350/7.5

=46.67 miles/hour.

Hence, the total distance he drove is 350 miles, with an average speed of 46.67 miles/hour.