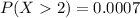Question

Find the probability that a person is audited more than twice. (Round your answer to four decimal places.)

Answer 1

Complete Question

The chance of an IRS audit for a tax return with over $25,000 in income is about 2% per year. We are interested in the expected number of audits a person with that income has in a 9-year period. Assume each year is independent.

Find the probability that a person is audited more than twice. (Round your answer to four decimal places.)

Answer:

The probability is
`P(X > 2) = 0.0007`

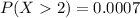
Explanation:

From the question we are told that

The probability of an IRS audit for a tax return with over $25,000 in income is p= 0.02

The sample size n = 9

Generally the distribution of IRS audit for a tax return follows a binomial distribution

i.e

`X  \~ \ \ \  B(n , p)`

and the probability distribution function for binomial distribution is

`P(X = x) =  ^(n)C_x *  p^x *  (1- p)^(n-x)`

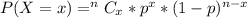
Here C stands for combination hence we are going to be making use of the combination function in our calculators

Generally the probability that a person is not audited at all is mathematically

`P(X = 0) =  ^(9)C_0 *  (0.02)^0 *  (1- 0.02 )^(9-0)`

`P(X = 0) =  ^(9)C_0 *  (0.02)^0 *  (0.98 )^(9-0)`

`P(X = 0) =  0.8337`

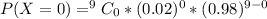
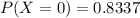
Generally the probability that a person is audited once is mathematically

`P(X = 1) =  ^(9)C_1 *  (0.02)^1 *  (1- 0.02 )^(9-1)`

`P(X = 1) =  9*  (0.02)^1 *  (0.98 )^(8)`

`P(X = 1) =  0.1531`

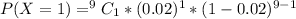
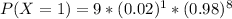
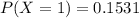
Generally the probability that a person is audited twice is mathematically represented

`P(X = 2) =  ^(9)C_2 *  (0.02)^2 *  (1- 0.02 )^(9-2)`

`P(X = 2) =  36 *  (0.02)^2 *  (0.98 )^(7)`

`P(X = 2) =  0.0125`

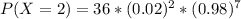
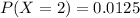
Generally the probability that a person is audited more than twice is mathematically represented

`P(X > 2) =  1 - [P(X = 0 ) + P(X = 1 )+ P(X =2)]`

=>
`P(X > 2) =  1 - [0.8337 + 0.1531+0.0125 ]`

=>
`P(X > 2) = 0.0007`