Question

A wire that is 80 centimeters long is shown below. The wire is cut into two pieces, and each piece is bent and formed into the shape of a square. 80 cm wire Suppose that the side length (in centimeters) of one square is x cm. Express the perimeter of the big square in terms of x. (1 point)

Answer 1

The perimeter of the second(big) square =
`\mathbf{4 * \begin {pmatrix} (80-x)/(4) \end {pmatrix}}`

Explanation:

From the information given:

The length of the piece of the wire = 80 cm

When being cut into two pieces;

the length of the first wire = x

Then the length of the second(big) wire will be = 80 - x

However, when each piece is bent to a square shape

The length of one side of the first square =
`(x)/(4)`

The length of one side of the second(big) square;
`(80-x)/(4)`

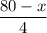
Area of a square = l² ( where l is the length of the sides)

For the first square

A₁ =
`((x)/(4))^2`

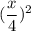
A₁ =
`(x^2)/(16)`

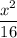
The area of the second(big) square is:

A₂ =
`((80-x)/(4))^2`

A₂ =
`(((80-x)^2)/(4))`

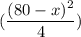
The perimeter of the first square =
`4 * (x)/(4)`

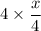
The perimeter of the second(big) square =
`\mathbf{4 * \begin {pmatrix} (80-x)/(4) \end {pmatrix}}`