Question

If the breaking strength of the string is 120 N, what is the minimum angle the string can make with the horizontal

Answer 1

Complete Question

A 940-g rock is whirled in a horizontal circle at the end of a 1.30-m-long string, If the breaking strength of the string is 120 N, what's the minimum angle the string can make with the horizontal?

Answer:

The value is
`\theta = 4.41^o`

Step-by-step explanation:

From the question we are told that

The mass of the rock is
`m_r = 940 \ g = 0.94 \ kg`

The length of the string is
`l = 1.30 \ m`

The breaking strength(i.e the maximum tension) on the string is
`T = 120 \ N`

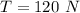
Gnerally the vertical component of the tension experienced by the string is mathematically represented as

`T_v = T sin(\theta)`

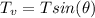
Generally this vertical component of tension is equivalent to the weight of the rock

So

`Tsin (\theta) = mg`

=>
`\theta = sin^(-1) [(mg)/( T) ]`

=>
`\theta = sin^(-1) [(0.940 *9.8 )/( 120) ]`

=>
`\theta = 4.41^o`