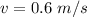Complete Question
A block is attached to one end of a spring with the other end of the spring fixed to a wall. The block is vibrating horizontally on a frictionless surface. If the mass of the block is 4.0 kg, the spring constant is k = 100 N/m, and the maximum distance of the block from the equilibrium position is 20 cm, what is the speed of the block at an instant when it is a distance of 16 cm from the equilibrium position?
Answer:
The velocity is
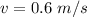
Step-by-step explanation:
From the question we are told that
The mass of the block is m = 4.0 kg
The spring constant is k = 100 N/m
The maximum distance of the block from equilibrium position is d = 20 cm =0.20 m
The distance considered is
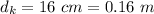
Generally the maximum energy stored in the spring is mathematically represented as
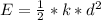
=>
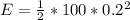
=>

Gnerally according to the law of energy conservation
The energy maximum energy of the spring = energy of the spring at
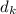 + energy of the block at
+ energy of the block at
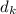
Here energy of the block at
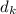 is mathematically represented as
is mathematically represented as
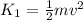
=>
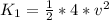
=>
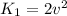
Generally the energy of the spring at
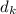 is mathematically represented as
is mathematically represented as
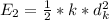
=>

=>
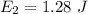
So
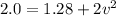
=>