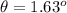Answer:
The value is
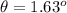
Step-by-step explanation:
From the question we are told that
The wavelength of the first spectral line is
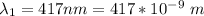
The wavelength of the second spectral line is
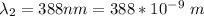
The diffraction grating is
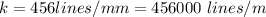
Generally the condition for constructive interference is
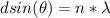
Here n is the order of maxima which is n = 2 given that order of the spectral lines is second order
d is this the distance of slit separation which is evaluated as
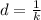
=>
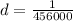
=>

Considering the first spectral lines with
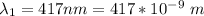
![\theta_1 = sin ^(-1) [( 2 * 417 * 10^(-9))/(2.19298 *10^(-6)) ]](https://img.qammunity.org/2021/formulas/physics/college/l0mqd8aybnq5msq7qeidmpgwemtqanggf2.png)
=>
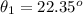
Considering the first spectral lines with
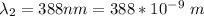
![\theta_2 = sin ^(-1) [( 2 * 388 * 10^(-9))/(2.19298 *10^(-6)) ]](https://img.qammunity.org/2021/formulas/physics/college/uzewgettrohmihx6lktk57vt4mmrooqzak.png)
=>
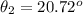
Generally the angular separation is
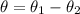
=>

=>