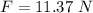Question

Two blocks, stacked one on top of the other, slide on a frictionless horizontal surface. The surface between the two blocks is rough, however, with a coefficient of static friction equal to 0.40. The top block has a mass of 2.9 kg, and the bottom block's mass is 5.8 kg. If a horizontal force F is applied to the bottom block, what is the maximum value F can have before the top block begins to slip?

Answer 1

The value is
`F = 11.37 \ N`

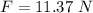
Step-by-step explanation:

From the question we are told that

The coefficient of static friction is
`\mu_s = 0.40`

The mass of the top of block is
`m_t = 2.9 \ kg`

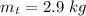
The mass of the bottom is
`m_b = 5.8 \ kg`

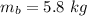
Generally given that the frictional force between the bottom block and the frictionless horizontal is zero then the maximum value F can have before the top block begins to slip will be equal to the frictional force between the top and the bottom block which is mathematically represented as

`F = F_f =\mu_s * N`

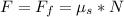
Here N is the normal force acting on top block which is mathematically represented as

`N = m_t * g`

`N = 2.9 * 9.8`

=>
`N = 28.42 \ N`

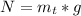
So

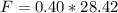
`F = 0.40 * 28.42`

=>
`F = 11.37 \ N`