Question

Oe is responsible for reserving hotel rooms for a company trip. His company changes plans and increases how many people are going on the trip, so they need at least 505050 total rooms. Joe had already reserved and paid for 161616 rooms, so he needs to reserve additional rooms. He can only reserve rooms in blocks, and each block contains 888 rooms and costs \$900$900dollar sign, 900. Let BBB represent the number of additional blocks that Joe reserves. 1) Which inequality describes this scenario? Choose 1 answer: Choose 1 answer: (Choice A) A 16+8B \leq 5016+8B≤5016, plus, 8, B, is less than or equal to, 50 (Choice B) B 16+8B \geq 5016+8B≥5016, plus, 8, B, is greater than or equal to, 50 (Choice C) C 16+B \leq 5016+B≤5016, plus, B, is less than or equal to, 50 (Choice D) D 16+B \geq 5016+B≥5016, plus, B, is greater than or equal to, 50 2) What is the least amount of additional money Joe can spend to get the rooms they need? dollars

Answer 1

Given:

They need at least 50 total rooms.

Already reserved rooms = 16

1 Block = 8 rooms

Cost of one block = $900

To find:

The inequality for the given scenario.

Solution:

(1)

Let B represent the number of additional blocks that Joe reserves.

1 Block = 8 rooms

B Block = 8B rooms

Total number of rooms = 16 + 8B

They need at least 50 total rooms. It means, total number of rooms must be great than or equal to 50.

`16+8B\geq 50`

Therefore, the correct option is B.

(2)

We have,

`8B\geq 50-16`

`8B\geq 34`

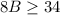
Divide both sides by 8.

`B\geq (34)/(8)`

`B\geq 4.25`

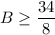
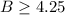
So, least number of required blocks is 5.

Least amount of additional money is

`5* \$900=\$4500`

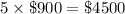
Therefore, the least amount of additional money Joe can spend to get the rooms they need is 4500 dollars.