Question

The water works commission needs to know the mean household usage of water by the residents of a small town in gallons per day. They would like the estimate to have a maximum error of 0.09 gallons. A previous study found that for an average family the variance is 5.29 gallons and the mean is 15.6 gallons per day. If they are using a 99% level of confidence, how large of a sample is required to estimate the mean usage of water? Round your answer up to the next integer.

Answer 1

4347

Explanation:

Given that:

The margin of error = 0.09

Variance
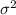`\sigma^2` = 5.29

Mean = 15.6

Level of significance = 0.99

The objective is to determine the sample size used in this study to estimate the mean usage of water.

From the given information:

The critical value
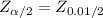`Z_(\alpha/2) = Z_(0.01/2)` = 2.58

Sample size n =
`Z_(\alpha/2)^2 * \begin{pmatrix} (\sigma^2)/(M.O.E^2) \end {pmatrix}`

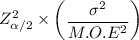
Sample size n =
`2.58^2 * \begin {pmatrix} (5.29)/(0.09^2)\end {pmatrix}`

Sample size n = 4347