Question

The drawing shows two planes each dropping an empty fuel tank. At the moment of release each plane has the same speed of 165 m/s, and each tank is at the same height of 3.38 km above the ground. Although the speeds are the same, the velocities are different at the instant of release, because one plane is flying at an angle of 15.0° above the horizontal and the other is flying at an angle of 15.0° below the horizontal. Find the (a) magnitude and (b) direction of the velocity with which the fuel tank hits the ground if it is from plane A. Find the (c) magnitude and (d) direction of the velocity with which the fuel tank hits the ground if it is from plane B. In each part, give the direction as a positive angle with respect to the horizontal.

Answer 1

(a) 305.83 m/s

(b) +89° to the horizontal

(c) 305.83 m/s

(d)+89° to the horizontal

Step-by-step explanation:

The speed of the (air)planes = 165 m/s

The height from which the planes release the fuel tank = 3.38 km

The direction of one of the plane (plane A) at the time of release = 15° above the horizontal

The direction of the other plane (plane B) at the time of release = 15° below the horizontal

(a) The velocity of the plane is given as follows;

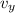`v_y` = v₀·sin(θ₀) - g·t

At maximum height,
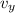`v_y` = 0

v₀·sin(θ₀) = g·t

t = 165×sin(15)/9.81 ≈ 4.35 s

The maximum height = 165×sin(15)×4.35 - 1/2×9.81×4.35 ² ≈ 92.95 m

The magnitude of the vertical velocity when the tank touches the ground is given as follows;

v² = u² - 2·g·s

u = 0

s = 3.38 + 0.09295 ≈ 3.47 km

v² = 2 × 9.81 × 3473

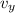`v_y` ≈ 261 m/s

The horizontal velocity = 165 × cos 15 ≈ 159.4 m/s

The magnitude = √(261² + 159.4²) ≈ 305.83 m/s

(b) The direction = tan^(-1)(261/159.4) ≈ 89° to the horizontal

(c) The time it takes the tank to reach the ground is given as follows;

v² = (165×sin(15))² + 2 × 9.81 × 3380 = 68139.33 m²/s²

v = 261.035 m/s

The horizontal velocity is the same as above = 159.4 m/s

The magnitude and direction will therefore be the same as for plane A which are

The magnitude = √(261² + 159.4²) ≈ 305.83 m/s

(d)The direction = tan^(-1)(261/159.4) ≈ 89° to the horizontal