Question

The mean weight of an adult is 6565 kilograms with a standard deviation of 1313 kilograms. If 9292 adults are randomly selected, what is the probability that the sample mean would be greater than 62.762.7 kilograms

Answer 1

Answer: 0.9554

Explanation:

Let
`\overline{X}` be the sample mean.

Given: Mean weight
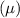`(\mu)` of an adult is 65 kilograms with a standard deviation
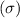`(\sigma)` of 13 kilograms.

Sample space = 92

The probability that the sample mean would be greater than 62.7 kilograms:

`P(\overline{X}>62.7)=P(\frac{\overline{X}-\mu}{(\sigma)/(√(n))}>(62.7-65)/((13)/(√(92))))\\\\=P(Z>-1.70)\\\\=P(Z<1.70)\ \ \ \[P(Z>-z)=P(Z<z)]\\\\=0.9554`[ By p-value table]

Hence, the required probability= 0.9554