Answer:
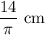
4.5 cm
Explanation:
If a straight line is bent into the shape of the circle the circumference of the circle will be equal to the straight line.
First circle's circumference is given by
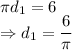
Second circle's circumference is given by

Total height of the pendant
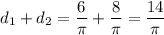
In terms of
 the height of the pendant is
the height of the pendant is
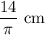
The height of the pendant is
