Options:
A. π is the area of a circle with a radius of 1.
B. π is the circumference of a circle with a radius of 1.
C. π is the constant of proportionality relating the radius of a circle to its area.
D. π is the circumference of a circle with a diameter of 1.
E. π is the constant of proportionality relating the diameter of a circle to its circumference.
Answer:
A, C, D, E
Explanation:
Analyzing the options, one after the other.
A.
Area is calculated as thus:
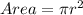
In this case,
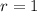
So: we have
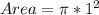
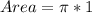
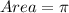
This option is true
B.
Circumference is calculated as thus:
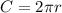
In this case
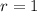
So, we have:
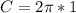
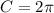
This option is false
C.
Area is calculated as thus:
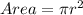
In this formula, Area and Radius can change but
 remains constant.
remains constant.
Hence, this option is true
D.
Circumference is calculated as thus:
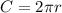 or
or
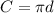
Where
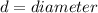
In this case
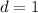
So, we have:
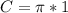
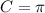
Hence, this option is true
E.
Circumference is calculated as thus:
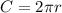 or
or
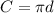
Where
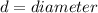
Considering
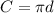
In this formula, Circumference and Diameter can change but
 remains constant.
remains constant.
Hence, this option is true