Question

Segment CD is formed by C(-5, 9) and D(7, 5). If line t is the perpendicular bisector of segment CD , write a linear equation for t in slope-intercept form.

Answer 1

Given:

Segment CD is formed by C(-5, 9) and D(7, 5).

Line t is the perpendicular bisector of segment CD.

To find:

The linear equation for t in slope-intercept form.

Solution:

Line t is the perpendicular bisector of segment CD. It means line t passes through the midpoint of CD.

`Midpoin=\left((x_1+x_2)/(2),(y_1+y_2)/(2)\right)`

`Midpoin=\left((-5+7)/(2),(9+5)/(2)\right)`

`Midpoin=\left((2)/(2),(14)/(2)\right)`

`Midpoin=\left(1,7\right)`

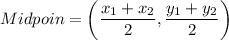
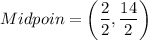
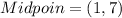
Slope of CD is

`m=(y_2-y_1)/(x_2-x_1)`

`m_(1)=(5-9)/(7-(-5))`

`m_(1)=(-4)/(12)`

`m_(1)=(-1)/(3)`

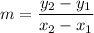
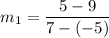
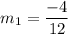
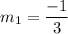
Product of slopes of two perpendicular lines is -1.

Let slope of line t be
`m_2`.

`m_1* m_2=-1`

`(-1)/(3)* m_2=-1`

`m_2=3`

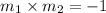
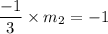
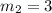
Point slope form of a line is

`y-y_1=m(x-x_1)`

where, m is slope.

The slope of line t is 3 and it passes through (1,7). So, point slope form of line t is

`y-7=3(x-1)`

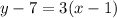
Therefore, the point slope form of line t is
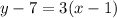`y-7=3(x-1)`.