Question

The numerator of a fraction is 1 less than the denominator.

When both numerator and denominator are increased by 2,
the fraction is increased by . Find the original fraction.

Answer 1

There is missing data in the problem, I have added it to solve the problem. You can use your real data once you understand the explanation.

Answer:

Original fraction:

`\displaystyle (5)/(6), \ (-9)/(-8)`

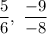
Explanation:

The numerator of a fraction is 1 less than the denominator and when both parts are increased by 2, the value of the fraction increases by 1/24. Find the original fraction.

Let's call:

x=original numerator

x+1=original denominator

x+2=increased numerator

x+3=increased denominator

Original fraction:

`\displaystyle (x)/(x+1)`

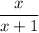
Increased fraction:

`\displaystyle (x+2)/(x+3)`

The difference between both is 1/24:

`\displaystyle (x+2)/(x+3)-(x)/(x+1)=(1)/(24)`

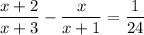
Multiply by (x+3)(x+1):

`\displaystyle (x+3)(x+1)(x+2)/(x+3)-(x+3)(x+1)(x)/(x+1)=((x+3)(x+1))/(24)`

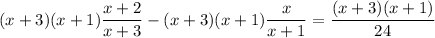
Simplifying each fraction when possible:

`\displaystyle (x+1)(x+2)-(x+3)(x)=((x+3)(x+1))/(24)`

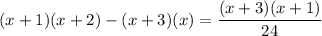
Operating:

`\displaystyle x^2+3x+2-x^2-3x=(x^2+4x+3)/(24)`

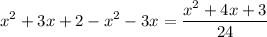
Simplifying:

`\displaystyle 2=(x^2+4x+3)/(24)`

Multiplying by 24:

`48=x^2+4x+3`

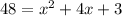
Rearranging:

`x^2+4x-45=0`

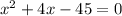
Factoring:

`(x-5)(x+9)=0`

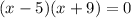
We have two solutions:

`x=5, x=-9`

Selecting the first solution:

Original fraction:

`\displaystyle (5)/(6)`

Increased fraction:

`\displaystyle (7)/(8)`

The difference between both is:

`\displaystyle (7)/(8)-(5)/(6)=(21-20)/(24)=(1)/(24)`

This is a valid solution

Selecting the second solution:

Original fraction:

`\displaystyle (-9)/(-8)=(9)/(8)`

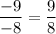
Increased fraction:

`\displaystyle (-7)/(-6)=(7)/(6)`

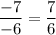
The difference between both is:

`\displaystyle (7)/(6)-(9)/(8)=(28-27)/(24)=(1)/(24)`

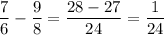
This solution is only valid if we express the fractions with their negative values. When we simplify them, the first condition is not met. Thus, the solutions are:

Original fraction:

`\displaystyle (5)/(6), \ (-9)/(-8)`

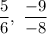
Note: The last solution can be arguable because the real simplified fraction is not a solution. My opinion is that it's valid as long as it's expressed with their original signs.