Answer:
Ranking:
326.4 m, 312.4 m, 186 m, 140.5 m, 86.6 m, 27.9 m
Step-by-step explanation:
Projectile Motion
It's known as the type of motion that experiences an object that is launched near the Earth's surface and moves along a curved path exclusively under the action of gravity.
Being vo the initial speed of the object, θ the initial launch angle, and g=9.8m/s^2 the acceleration of gravity, then the maximum vertical height the object reaches is calculated by:
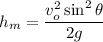
We have to test for different launching angles and sort the maximum heights from lowest to highest. For all the test cases, vo=80 m/s.

h=86.6 m
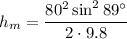
h=326.4 m
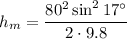
h=27.9 m
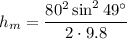
h=186 m
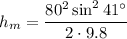
h=140.5 m
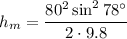
h=312.4 m
Ranking:
326.4 m, 312.4 m, 186 m, 140.5 m, 86.6 m, 27.9 m