9514 1404 393
Answer:
{ (-441/23, 433/23) }
Explanation:
The "cross-multiplication method" is usually shown as follows:
1. rewrite the equations in general form: ax +by +c = 0
2. write the coefficients in two row in the order b, c, a, b.
3. form three products, each being the number in the first row times the number to its right in the second row. That is, b1·c2, c1·a2, a1·b2
4. form three more products, each being the number in the second row times the number to its right in the first row. That is, b2·c1, c2·a1, a2·b1
5. form three differences, subtracting the products of step 4 from those of step 3. Call these differences d1, d2, d3. (For example, d1=b1c2-b2c1.)
6. The values of x and y satisfy the equations ...
x/d1 = y/d2 = 1/d3
which is to say, ...
x = d1/d3, and y = d2/d3
_____
For your equations, we can rewrite them as ...
- 11x +12y -15 = 0
- 12x +11y +23 = 0
Then our rows of coefficients are ...
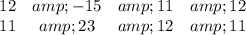
And our differences are ...
d1 = 12(23) -11(-15) = 441
d2 = -15(12) -23(11) = -433
d3 = 11(11) -12(12) = -23
The relations between x and y are ...
x/441 = y/-433 = 1/-23
so, x = -441/23 and y = 433/23
The solution set is one ordered pair: { (-441/23, 433/23) }.
_____
Additional comments
The final solution is identical to the formula arrived at using Cramer's Rule. Calling this the "cross-multiplication method" avoids any discussion of matrices and determinants.