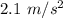Answer:
horizontal component:
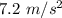
vertical component:
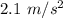
Step-by-step explanation:
Rectangular components of a vector
Given a vector as a (magnitude, angle) pair, the rectangular components can be calculated as:
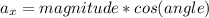
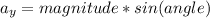
The acceleration of the airplane is given with a magnitude of 7.5 m/s^2 and an angle of 16°.
Calculate the components:
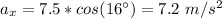
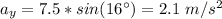
horizontal component:
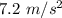
vertical component: