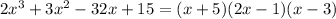Question

Factor f(x) = 2x^3 + 3x^2 - 32x+ 15 into linear factors given that - 5 is a zero of f(x)

Answer 1

`2x^3+3x^2-32x+15=(x+5)(2x-1)(x-3)`

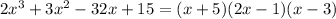
Explanation:

If "-5" is a zero of the function, then we know that the binomial (x+5) divides perfectly our cubic expression.

By using division of polynomials we find that :

`f(x) = (x+5)*(2x^2-7x+3)`

and now we proceed to factor out the trinomial :

`2x^2-7x+3 = 2x^2-6x-x+3 =\\2x(x-3)-(x-3)= (2x-1)(x-3)`

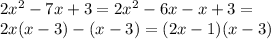
Therefore the full factorization is:

`2x^3+3x^2-32x+15=(x+5)(2x-1)(x-3)`