Question

Solve this equation algebraically.

Answer 1

Write both sides as powers of 16:

`\log_4(2-x)=\log_(16)(13-4x) \implies 16^(\log_4(2-x))=16^{\log_(16)(13-4x)}`

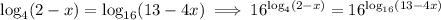
Since 16 = 4², we can rearrange the left side to get

`16^(\log_4(2-x))=(4^2)^(\log_4(2-x))=4^(2\log_4(2-x))=4^(\log_4(2-x)^2)`

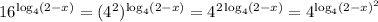
Then, recalling that
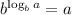`b^(\log_ba)=a`, we have

`4^(\log_4(2-x)^2)=16^{\log_(16)(13-4x)}\implies(2-x)^2=13-4x`

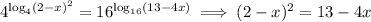
Now solve for x :

`(2-x)^2=13-4x`

`4-4x+x^2=13-4x`

`x^2-9=0`

`(x+3)(x-3)=0`

`\implies x=-3\text{ or }x=3`

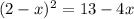
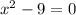
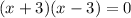
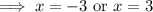
Notice that if x = 3, then log₄(2 - x) = log₄(-1) is undefined, so we throw out this solution. We don't run into this problem with x = -3, so that's the only (real) solution.