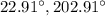Question

Why are there two values of theta if tan theta = 0.4226

Answer 1

`22.91^\circ, 202.91^\circ`

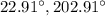
Explanation:

Given that:

`tan\theta=0.4226`

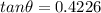
To find:

The two values of
`\theta = ?`

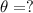
Solution:

By given equation:

`\theta = tan^(-1)(0.4226)`

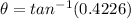
`\theta` can be equal to
`\approx 20.91^\circ`

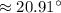
Also, we know the property that,
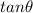`tan\theta` is positive in the 3rd quadrant.

and following is also true:

`tan\theta = tan(180^\circ+\theta)`

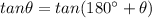
Therefore, another value possible for
`\theta` can be:

`\theta =180^\circ+22.91\\\Rightarrow \theta \approx 202.91^\circ`

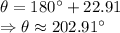
Therefore, the answer is:

`22.91^\circ, 202.91^\circ`