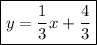Question

Write an equation of the line in slope-intercept form.

Answer 1

`\displaystyle y=(1)/(3)x+(4)/(3)`

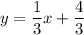
Explanation:

Equation of a line

The slope-intercept form of a line is:

y=mx+b

Where m is the slope and b is the y-intercept.

Suppose we know the line passes through points A(x1,y1) and B(x2,y2). The slope can be calculated as follows:

`\displaystyle m=(y_2-y_1)/(x_2-x_1)`

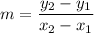
Two points are given: (-4,0) (2,2). Calculate the slope:

`\displaystyle m=(2-0)/(2+4)=(2)/(6)=(1)/(3)`

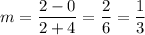
We'll use the point-slope form of the line:

y-k=m(x-h)

Take the point (2,2):

`\displaystyle y-2=(1)/(3)(x-2)`

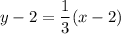
Operating:

`\displaystyle y-2=(1)/(3)x-(2)/(3)`

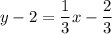
Adding 2:

`\displaystyle y=(1)/(3)x-(2)/(3)+2`

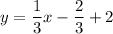
Operating, we get the slope-intercept form:

`\boxed{\displaystyle y=(1)/(3)x+(4)/(3)}`