Answer:
The system of equations is y = x - 4 and y = x² - 6
Explanation:
The graph has a linear equation represented by a line and a quadratic equation represented by a parabola
The form of the linear equation is y = m x + b, where m is the slope and b is the y-intercept
The form of the quadratic equation is y = a(x - h)² + k, where (h, k) are the coordinates of its vertex point and a is the coefficient of x²
let us use the graph to find each equation
→ Equation the line
∵ The line passes through points (-1, -5) and (2, -2)
∵ m =
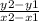
∴ m =
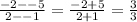
∴ m = 1
∵ The line intersected the y-axis at point (0, -4)
∵ b is the value of y at x = 0
∴ b = -4
→ Substitute the values of m and b in the form of the equation above
∴ y = (1)x + (-4)
∴ y = x - 4
→ Equation the parabola
∵ The vertex of the parabola is (0, -6)
∴ h = 0 and k = -6
→ Substitute them in the equation
∴ y = a(x - 0)² + -6
∴ y = ax² - 6
→ To find a choose any point on the parabola and substitute x and y
by its coordinated
∵ The point (2, -2) lies on the parabola
∴ x = 2 and y = -2
∵ -2 = a(2)² - 6
∴ -2 = 4a - 6
→ Add 6 to both sides
∵ -2 + 6 = 4a - 6 + 6
∴ 4 = 4a
→ Divide both sides by 4
∴ 1 = a
∴ y = (1)x² - 6
∴ y = x² - 6
The system of equations is y = x - 4 and y = x² - 6